Sort 排序算法
Quick Sort 快速排序
快速排序(Quick Sort)是一种基于分治法的排序算法。
- 时间复杂度:平均 O(nlogn)
- 空间复杂度:平均 O(logn)
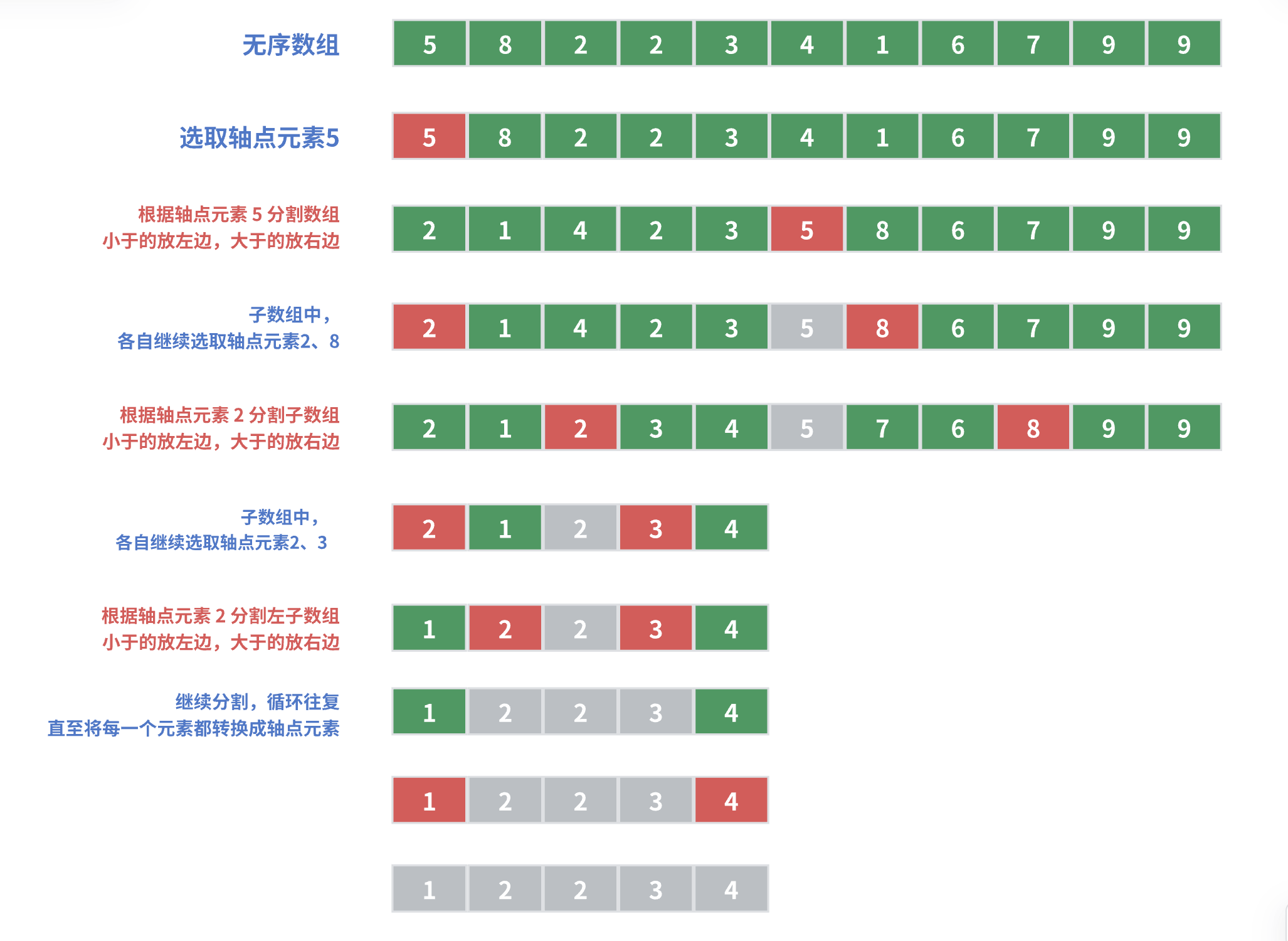
其基本思想是通过一个“轴点”元素(pivot)将待排序的数组分成两个子数组,分别对这两个子数组进行递归排序,从而达到整个数组有序。
实现步骤
- 从数组中选择一个轴点元素(pivot)
- 假设每次选择 0 位置的元素为轴点元素
- 根据轴点元素将数组分割为两个子数组:小于的放左边,大于的放右边
- 等于pivot的元素放哪边都可以
- 对子数组进行1、2操作
- 循环往复,直至将每一个元素都转换成轴点元素
- 此时,数组即完成排序
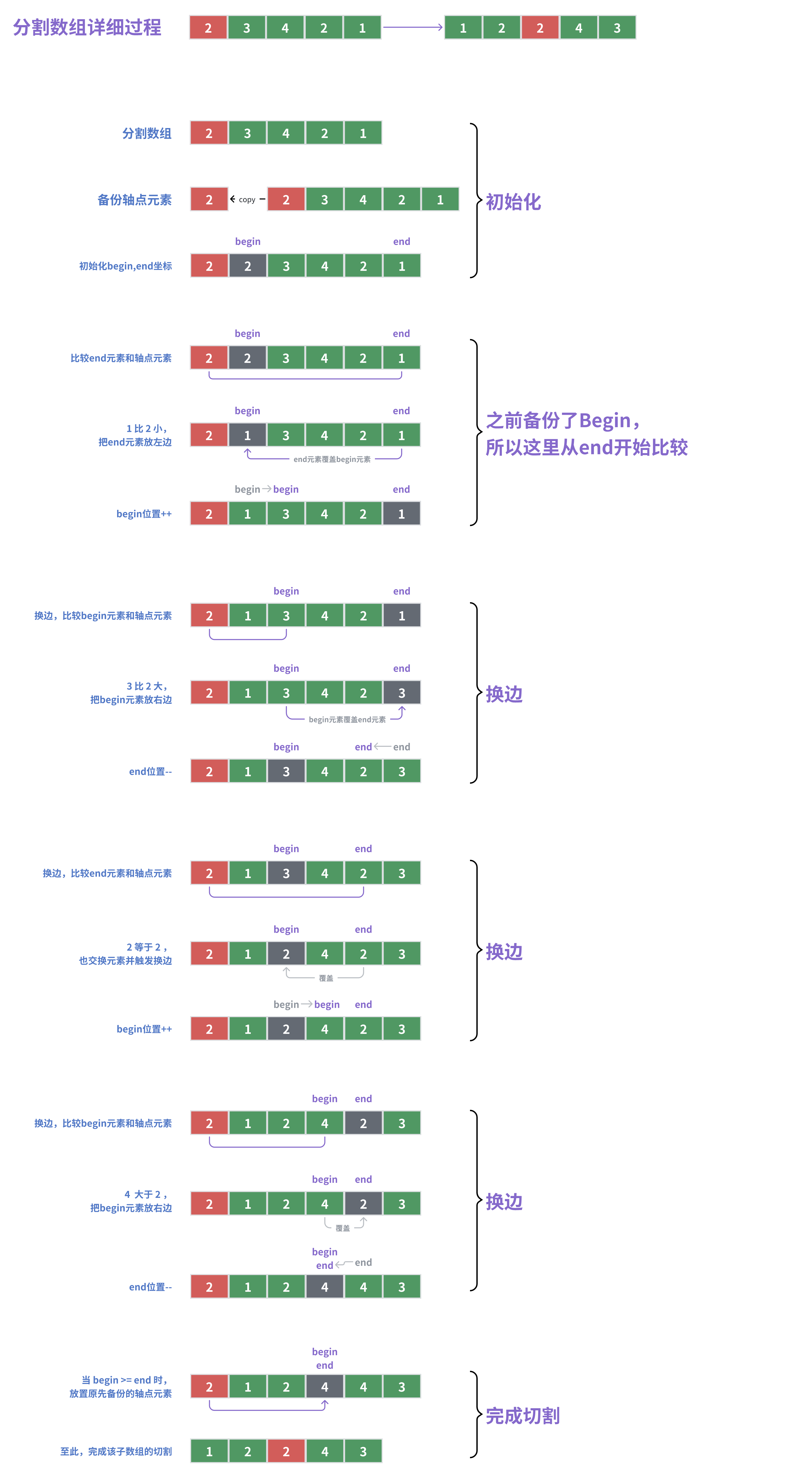
分割数组详细过程
根据轴点元素将数组分割为两个子数组
放置规则:小于的放左边,大于的放右边
等于轴点元素的放哪边都可以,但是要触发换边(为了保证左右子数组长度的均衡)
视频动画演示:https://www.douyin.com/user/self?from_tab_name=main&modal_id=7445221354938305852
轴点元素取值优化
优化轴点元素取值策略,防止极端情况。
假如输入数组是完全倒序的:54321
- 如果按默认取值 0号位置/begin位置 的元素为轴点元素,即取值5。
- 那么根据左小右大的分区规则,切割后的右子数组长度会为0,全部元素都被分配到左子数组上,分治策略即变相失效。
- O(logn)效率会退化为O(n),类似冒泡排序。
解决方案:尽量保证轴点元素是当前数组中的中位值(三数取中法)。
- 传递当前数组 头、中、尾 三个元素的下标
- 选取其中的中位数作为轴点元素,降低极端情况发生的概率
- 例如入参数组(54321)值中,会选取3作为轴点元素
代码实现
sort 递归排序
java
/**
* 快速排序(一种基于分治策略的排序算法)
* @param arr
* @param begin 对 [begin, end) 范围的元素进行快速排序
* @param end
*/
private void sort(int[] arr,int begin,int end) {
// 子数组长度为 1 时终止递归
if(begin >= end) return;
// 选取轴点元素,并切割数组
// 根据轴点元素分割为两个子数组:小于的放左边,大于的放右边
int pivotIndex = this.partition(arr,begin,end);
// 继续分割,循环往复,直至将每一个元素都转换成轴点元素
this.sort(arr,begin,pivotIndex -1);
this.sort(arr,pivotIndex + 1,end);
}partition 切割数组
java
/**
* 选取轴点元素,并切割数组
* @param arr
* @param begin
* @param end
* @return
*/
private int partition(int[] arr, int begin, int end) {
// 默认选择begin位置为轴点元素,并备份
int pivotIndex = this.smartBeginIndex(arr,begin,end);
int pivotValue = arr[pivotIndex];
// =========== 根据轴点元素分割为两个子数组:小于的放左边,大于的放右边
while(begin < end){ // 遍历所有元素
// =========== 逐一和轴点元素比较,从右边end开始(因为上方pivotValue备份的是begin位置的元素)
while(begin < end){
if(arr[end] > pivotValue){ // end元素 大于 pivot:即在正确的位置上,不需要触发交换,end--继续比较下一个元素即可
end--;
}else{
// end元素 小于或者等于 pivot:触发交换,end元素需放置左边begin元素的位置上
/**
* 原先begin位置的元素在上方已经被备份了,所以此处end元素可以覆盖begin位置的元素
**/
this.swap(arr,begin,end);
begin++; // 更新begin位置
break; // 并换边,从begin位置开始比较
}
}
//换边
while(begin < end){
if(arr[begin] < pivotValue){
begin++; //begin元素小于pivot,处于合适位置,继续比较下一个begin++元素
}else{
// begin元素 大于或者等于 pivot:触发交换,begin元素需放置右边end元素的位置上
this.swap(arr,begin,end);
end--;
break; // 换边
}
}
}
// 遍历结束后,把轴点元素 放置 在begin/end的位置上
arr[begin] = pivotValue;
return begin; //返回轴点元素下标,begin/end都可以
}
private void swap(int[] arr, int begin, int end) {
int temp = arr[begin];
arr[begin] = arr[end];
arr[end] = temp;
}smartBeginIndex 轴点元素取值
java
/**
* 默认选择begin位置为轴点元素下标
* - 优化轴点元素取值策略,防止极端情况(例如输入数组是完全倒序的)
* @return
*/
private int smartBeginIndex(int[] arr, int begin, int end) {
// return begin;
/**
* 例如输入数组是完全倒序的:54321
* - 如果取值begin位置元素为轴点元素,即5。
* - 那么切割后的右子数组长度会为0,全部元素都被分配到左子数组上,分治策略失效。
* - O(logn)效率会退化为O(n),类似冒泡排序。
*
* 解决方案:尽量保证轴点元素是当前数组中的中位值。
* - 传递当前数组 头、中、尾 三个元素的下标
* - 选取其中的中位数作为轴点元素,降低极端情况发生的概率
*/
int midIndex = this.medianPivot(arr, begin, (begin + end) >> 1, end);
// 注意将中位数交换至数组最左端,避免影响后续实现
this.swap(arr,begin,midIndex);
return begin;
}
/**
* 取数组指定下标位置的中位值
* @return index
*/
private int medianPivot(int[] arr, int begin,int mid,int end){
int b = arr[begin], m = arr[mid], e = arr[end];
if((m >= b && m <= e) || (m <= b && m >= e)) // 123、321
return mid; // m 在 b 和 e 之间
if((b >= m && b <= e) || (m >= b && b >= e)) // 213、231
return begin; // b 在 m 和 e 之间
return end;
}完整代码实现
QuickSort 完整代码实现
java
package algorithm.sort;
import org.junit.Test;
/**
* @author XRZ
* @version 1.00
* @Date 2025/2/22 11:19
*/
public class QuickSortTest {
@Test
public void test(){
// https://blog.csdn.net/weixin_43734095/article/details/105156039
int[] arr = {2,1,6,3,5,4,7,8,9,9,1};
this.sort(arr,0,arr.length - 1);
for (int i : arr) {
System.out.println(i);
}
}
/**
* 快速排序(一种基于分治策略的排序算法)
* @param arr
* @param begin 对 [begin, end) 范围的元素进行快速排序
* @param end
*/
private void sort(int[] arr,int begin,int end) {
// 子数组长度为 1 时终止递归
if(begin >= end) return;
// 选取轴点元素,并切割数组
// 根据轴点元素分割为两个子数组:小于的放左边,大于的放右边
int pivotIndex = this.partition(arr,begin,end);
// 继续分割,循环往复,直至将每一个元素都转换成轴点元素
this.sort(arr,begin,pivotIndex -1);
this.sort(arr,pivotIndex + 1,end);
}
/**
* 选取轴点元素,并切割数组
* @param arr
* @param begin
* @param end
* @return
*/
private int partition(int[] arr, int begin, int end) {
// 默认选择begin位置为轴点元素,并备份
int pivotIndex = this.smartBeginIndex(arr,begin,end);
int pivotValue = arr[pivotIndex];
// =========== 根据轴点元素分割为两个子数组:小于的放左边,大于的放右边
while(begin < end){ // 遍历所有元素
// =========== 逐一和轴点元素比较,从右边end开始(因为上方pivotValue备份的是begin位置的元素)
while(begin < end){
if(arr[end] > pivotValue){ // end元素 大于 pivot:即在正确的位置上,不需要触发交换,end--继续比较下一个元素即可
end--;
}else{
// end元素 小于或者等于 pivot:触发交换,end元素需放置左边begin元素的位置上
/**
* 原先begin位置的元素在上方已经被备份了,所以此处end元素可以覆盖begin位置的元素
**/
this.swap(arr,begin,end);
begin++; // 更新begin位置
break; // 并换边,从begin位置开始比较
}
}
//换边
while(begin < end){
if(arr[begin] < pivotValue){
begin++; //begin元素小于pivot,处于合适位置,继续比较下一个begin++元素
}else{
// begin元素 大于或者等于 pivot:触发交换,begin元素需放置右边end元素的位置上
this.swap(arr,begin,end);
end--;
break; // 换边
}
}
}
// 遍历结束后,把轴点元素 放置 在begin/end的位置上
arr[begin] = pivotValue;
return begin; //返回轴点元素下标,begin/end都可以
}
private void swap(int[] arr, int begin, int end) {
int temp = arr[begin];
arr[begin] = arr[end];
arr[end] = temp;
}
/**
* 默认选择begin位置为轴点元素下标
* - 优化轴点元素取值策略,防止极端情况(例如输入数组是完全倒序的)
* @return
*/
private int smartBeginIndex(int[] arr, int begin, int end) {
// return begin;
/**
* 例如输入数组是完全倒序的:54321
* - 如果取值begin位置元素为轴点元素,即5。
* - 那么切割后的右子数组长度会为0,全部元素都被分配到左子数组上,分治策略失效。
* - O(logn)效率会退化为O(n),类似冒泡排序。
*
* 解决方案:尽量保证轴点元素是当前数组中的中位值。
* - 传递当前数组 头、中、尾 三个元素的下标
* - 选取其中的中位数作为轴点元素,降低极端情况发生的概率
*/
int midIndex = this.medianPivot(arr, begin, (begin + end) >> 1, end);
// 注意将中位数交换至数组最左端,避免影响后续实现
this.swap(arr,begin,midIndex);
return begin;
}
/**
* 取数组指定下标位置的中位值
* @return index
*/
private int medianPivot(int[] arr, int begin,int mid,int end){
int b = arr[begin], m = arr[mid], e = arr[end];
if((m >= b && m <= e) || (m <= b && m >= e)) // 123、321
return mid; // m 在 b 和 e 之间
if((b >= m && b <= e) || (m >= b && b >= e)) // 213、231
return begin; // b 在 m 和 e 之间
return end;
}
}其它排序
冒泡排序
视频动画演示
https://www.douyin.com/user/self?from_tab_name=main&modal_id=7368479698277436711
代码实现
java
// XRZ-TODO 冒泡排序:选择最大的数往后排
void bubbleSortFromLeft(int[] arr) {
int length = arr.length;
//外循环:倒序循环,选择最大的数往后排(冒泡)
// i > 0; 头尾都可预留一位,无需比较(内循环会覆盖到)
for (int i = length - 1; i > 0; i--) { // 从右往左
//截止条件中:j不能等于i,要给下方[j+1]预留一位
for (int j = 0; j < i; j++) {
//内循环:逐一比较相邻的两个元素,将最大的数往后排
if(arr[j] > arr[j +1]){
swap(arr, j, j +1);
}
}
}
}
/**
* 使用异或运算符交换arr中的a和b
* @param arr
* @param a
* @param b
*/
void swap(int[] arr, int a,int b){
arr[a] = arr[a] ^ arr[b];
arr[b] = arr[a] ^ arr[b]; // arr[a] = a ^ b
arr[a] = arr[a] ^ arr[b];
}代码实现(标志优化)
java
/* 冒泡排序(标志优化) */
void bubbleSortWithFlag2(int[] nums) {
// 外循环:未排序区间为 [0, i]
for (int i = nums.length - 1; i > 0; i--) {
boolean flag = false; // 初始化标志位
// 内循环:将未排序区间 [0, i] 中的最大元素交换至该区间的最右端
for (int j = 0; j < i; j++) {
if (nums[j] > nums[j + 1]) {
// 交换 nums[j] 与 nums[j + 1]
int tmp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = tmp;
flag = true; // 记录交换元素
}
}
if (!flag)
break; // 此轮“冒泡”未交换任何元素,直接跳出
}
// {1,2,3,5,6,7,10,9,8} 这种情况下,在外循环i=7时就会跳出循环,返回结果。
// 如果内循环一次都没有触发交换,则说明已经是有序的了,无需再替换。
// 使用break跳出循环,减少不必要的比较。
}插入排序
视频动画演示
https://www.douyin.com/user/self?from_tab_name=main&modal_id=7368040191535189287
代码实现
java
// XRZ-TODO 插入排序:假设0号位有序,从1号位开始,把未排序的值(从左到右)逐一比较 插入到已排序的区间。(类似整理扑克牌)
void insertionSortFromLeft(int[] arr) {
int length = arr.length;
//外循环,从左到右,循环未排序的区间
// i 表示待比较的数(未排序的值)
// 头尾都可预留一位
// 0号位假设有序,无需比较,所以从1开始
// i不能等于length,要给下方arr[j+1]预留一位
for (int i = 1; i < length; i++) {
//内循环,从右到左,循环比较已排序的区间
// j >= 0 是为了触发0号位和1号位的比较
for (int j = i-1; j >= 0; j--) {
// 逐一比较最小值,把最小值往左插
// arr[j] = 已排序的值
// arr[j+1] = 未排序的值
if(arr[j] > arr[j+1]){
swap(arr,j,j+1);
}
}
}
}选择排序
代码实现
java
// XRZ-TODO 选择排序:选择最小的数 往左边排
void selectSortFromLeft(int[] arr) {
int length = arr.length;
// 外循环,循环未排序区间
// i < length - 1 此处最后一次不需要比较了,应为上一次的j循环已经比较过了
for (int i = 0; i < length - 1; i++) {
//记录最小值下标,假设0是最小值
int minIndex = i;
// 从1开始比较。每次循环未排序区间 寻找最小值放至 左边已排序区
for (int j = i + 1; j < length; j++) {
//内循环寻找最小值
if(arr[j] < arr[minIndex]){
// 更新最小值下标
minIndex = j;
}
swap(arr,i,minIndex);
}
}
}
void swap(int[] arr, int a,int b){
int t = arr[a];
arr[a] = arr[b];
arr[b] = t;
}